Coherence (physics)
In physics, coherence expresses the potential for two waves to interfere. Two monochromatic beams from a single source always interfere.[1]: 286 Physical sources are not strictly monochromatic: they may be partly coherent. Beams from different sources are mutually incoherent.
For other uses, see Coherence.
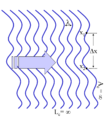
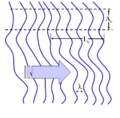
When interfering, two waves add together to create a wave of greater amplitude than either one (constructive interference) or subtract from each other to create a wave of minima which may be zero[1]: 286 (destructive interference), depending on their relative phase. Constructive or destructive interference are limit cases, and two waves always interfere, even if the result of the addition is complicated or not remarkable.
Two waves with constant relative phase will be coherent.[2] The amount of coherence can readily be measured by the interference visibility, which looks at the size of the interference fringes relative to the input waves (as the phase offset is varied); a precise mathematical definition of the degree of coherence is given by means of correlation functions. More generally, coherence describes the statistical similarity of a field (electromagnetic field, quantum wave packet etc.) at two points in space or time.[3]
Coherence and correlation[edit]
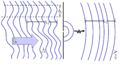
The coherence of two waves expresses how well correlated the waves are as quantified by the cross-correlation function.[7][1][8][9][10] Cross-correlation quantifies the ability to predict the phase of the second wave by knowing the phase of the first. As an example, consider two waves perfectly correlated for all times (by using a monochromatic light source). At any time, the phase difference between the two waves will be constant. If, when they are combined, they exhibit perfect constructive interference, perfect destructive interference, or something in-between but with constant phase difference, then it follows that they are perfectly coherent. As will be discussed below, the second wave need not be a separate entity. It could be the first wave at a different time or position. In this case, the measure of correlation is the autocorrelation function (sometimes called self-coherence). Degree of correlation involves correlation functions.[11]: 545-550
These states are unified by the fact that their behavior is described by a wave equation or some generalization thereof.
In system with macroscopic waves, one can measure the wave directly. Consequently, its correlation with another wave can simply be calculated. However, in optics one cannot measure the electric field directly as it oscillates much faster than any detector's time resolution.[12] Instead, one measures the intensity of the light. Most of the concepts involving coherence which will be introduced below were developed in the field of optics and then used in other fields. Therefore, many of the standard measurements of coherence are indirect measurements, even in fields where the wave can be measured directly.
Figure 6: A wave with a varying profile (wavefront) and infinite coherence length.
Figure 7: A wave with a varying profile (wavefront) and finite coherence length.
Figure 8: A wave with finite coherence area is incident on a pinhole (small aperture). The wave will diffract out of the pinhole. Far from the pinhole the emerging spherical wavefronts are approximately flat. The coherence area is now infinite while the coherence length is unchanged.
Figure 9: A wave with infinite coherence area is combined with a spatially shifted copy of itself. Some sections in the wave interfere constructively and some will interfere destructively. Averaging over these sections, a detector with length D will measure reduced interference visibility. For example, a misaligned Mach–Zehnder interferometer will do this.
Applications[edit]
Holography[edit]
Coherent superpositions of optical wave fields include holography. Holographic photographs have been used as art and as difficult to forge security labels.
Non-optical wave fields[edit]
Further applications concern the coherent superposition of non-optical wave fields. In quantum mechanics for example one considers a probability field, which is related to the wave function (interpretation: density of the probability amplitude). Here the applications concern, among others, the future technologies of quantum computing and the already available technology of quantum cryptography. Additionally the problems of the following subchapter are treated.
Modal analysis[edit]
Coherence is used to check the quality of the transfer functions (FRFs) being measured. Low coherence can be caused by poor signal to noise ratio, and/or inadequate frequency resolution.