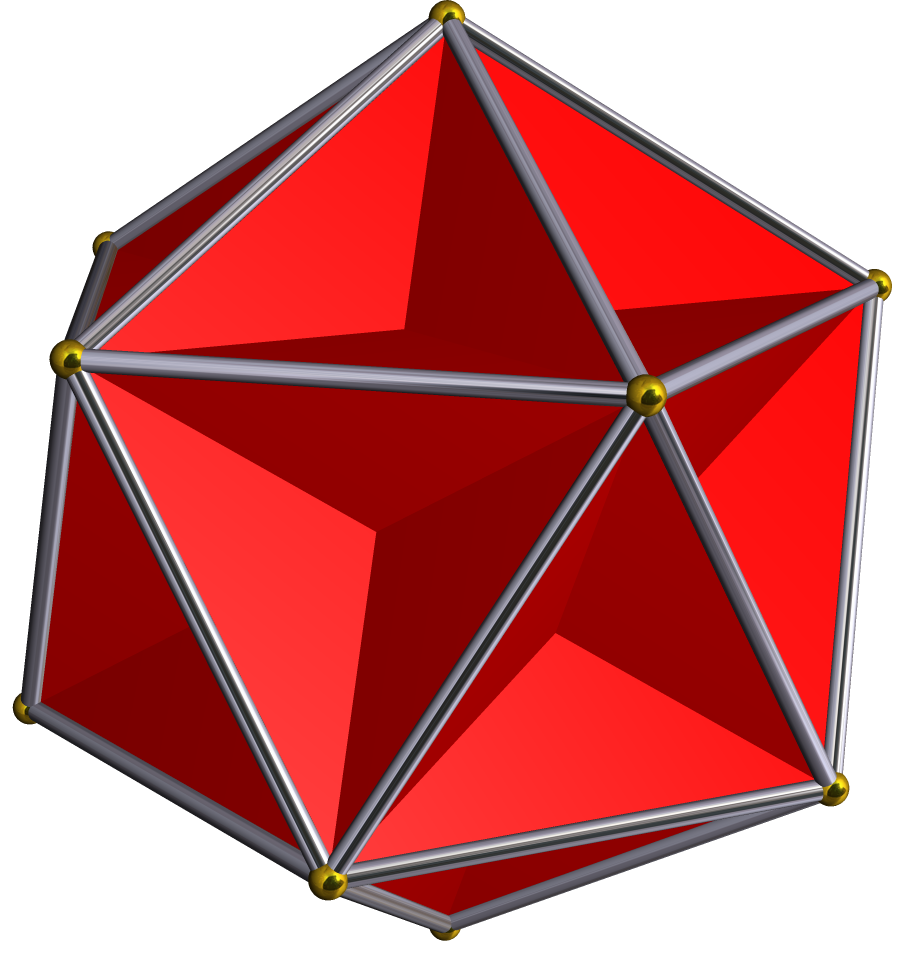
Great dodecahedron
In geometry, the great dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol {5,5/2} and Coxeter–Dynkin diagram of 
. It is one of four nonconvex regular polyhedra. It is composed of 12 pentagonal faces (six pairs of parallel pentagons), intersecting each other making a pentagrammic path, with five pentagons meeting at each vertex.
The discovery of the great dodecahedron is sometimes credited to Louis Poinsot in 1810, though there is a drawing of something very similar to a great dodecahedron in the 1568 book Perspectiva Corporum Regularium by Wenzel Jamnitzer.
The great dodecahedron can be constructed analogously to the pentagram, its two-dimensional analogue, via the extension of the (n – 1)-pentagonal polytope faces of the core n-polytope (pentagons for the great dodecahedron, and line segments for the pentagram) until the figure again closes.