Musical system of ancient Greece
The musical system of ancient Greece evolved over a period of more than 500 years from simple scales of tetrachords, or divisions of the perfect fourth, into several complex systems encompassing tetrachords and octaves, as well as octave scales divided into seven to thirteen intervals.[1]
This article is about the music theory and musical intervals used in ancient Greece. For a discussion of the cultural aspects and history of ancient Greek music, see Music of ancient Greece.Any discussion of the music of ancient Greece, theoretical, philosophical or aesthetic, is fraught with two problems: there are few examples of written music, and there are many, sometimes fragmentary, theoretical and philosophical accounts. The empirical research of scholars like Richard Crocker,[2][3][4] C. André Barbera,[5][6] and John Chalmers[7] has made it possible to look at the ancient Greek systems as a whole without regard to the tastes of any one ancient theorist. The primary genera they examine are those of Pythagoras and the Pythagorean school, Archytas, Aristoxenos, and Ptolemy (including his versions of the genera of Didymos and Eratosthenes).[8]
After the discovery of the fundamental intervals (octave, fourth and fifth), the first known systematic divisions of the octave were those of Pythagoras to whom was often attributed the discovery that the frequency of a vibrating string is inversely proportional to its length. Pythagoras construed the intervals arithmetically, allowing for 1:1 = Unison, 2:1 = Octave, 3:2 = Fifth, 4:3 = Fourth. Pythagoras's scale consists of a stack of perfect fifths, the ratio 3:2 (see also Pythagorean Interval and Pythagorean Tuning).
The earliest such description of a scale is found in Philolaus fr. B6. Philolaus recognizes that, if the interval of a fourth goes up from any given note, and then up the interval of a fifth, the final note is an octave above the first note. Thus, the octave is made up of a fourth and a fifth. ... Philolaus's scale thus consisted of the following intervals: 9:8, 9:8, 256:243 [these three intervals take us up a fourth], 9:8, 9:8, 9:8, 256:243 [these four intervals make up a fifth and complete the octave from our starting note]. This scale is known as the Pythagorean diatonic and is the scale that Plato adopted in the construction of the world soul in the Timaeus (36a-b).[12]
The next notable Pythagorean theorist known today is Archytas, contemporary and friend of Plato, who explained the use of arithmetic, geometric and harmonic means in tuning musical instruments. Euclid further developed Archytas's theory in his The Division of the Canon (Katatomē kanonos, the Latin Sectio Canonis). He elaborated the acoustics with reference to the frequency of vibrations (or movements).[13]
Archytas provided a rigorous proof that the basic musical intervals cannot be divided in half, or in other words, that there is no mean proportional between numbers in super-particular ratio (octave 2:1, fourth 4:3, fifth 3:2, 9:8).[12][14]
Archytas was also the first ancient Greek theorist to provide ratios for all 3 genera.[1] The three genera of tetrachords recognized by Archytas have the following ratios:
These three tunings appear to have corresponded to the actual musical practice of his day.[14]
The genera arose after the framing interval of the tetrachord was fixed, because the two internal notes (called lichanoi and parhypate) still had variable tunings. Tetrachords were classified into genera depending on the position of the lichanos (thus the name lichanos, which means "the indicator"). For instance a lichanos that is a minor third from the bottom and a major second from the top, defines the genus diatonic. The other two genera, chromatic and enharmonic, were defined in similar fashion.[15]
More generally, three genera of seven octave species can be recognized, depending on the positioning of the interposed tones in the component tetrachords:
Within these basic forms, the intervals of the chromatic and diatonic genera were varied further by three and two "shades" (chroai), respectively .[17][18]
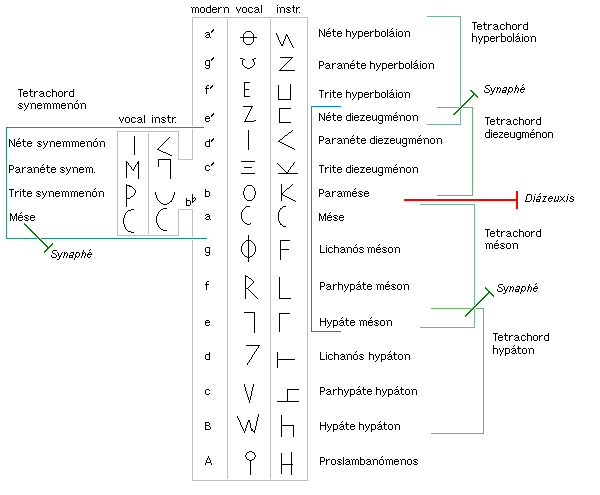
The elaboration of tetrachords was also accompanied by penta- and hexachords. The joining of a tetrachord and a pentachord yields an octachord, i.e. the complete seven-tone scale plus a higher octave of the base note. However, this was also produced by joining two tetrachords, which were linked by means of an intermediary or shared note. The final evolution of the system did not end with the octave as such but with the Systema teleion, a set of five tetrachords linked by conjunction and disjunction into arrays of tones spanning two octaves, as explained above.[1]
Ptolemy and the Alexandrians[edit]
In marked contrast to his predecessors, Ptolemy's scales employed a division of the pyknon in the ratio of 1:2, melodic, in place of equal divisions.[29] Ptolemy, in his Harmonics, ii.3–11, construed the tonoi differently, presenting all seven octave species within a fixed octave, through chromatic inflection of the scale degrees (comparable to the modern conception of building all seven modal scales on a single tonic). In Ptolemy's system, therefore there are only seven tonoi.[18][30] Ptolemy preserved Archytas's tunings in his Harmonics as well as transmitting the tunings of Eratosthenes and Didymos and providing his own ratios and scales.[1]
Ethos[edit]
The ancient Greeks have used the word ethos (ἔθος or ἦθος), in this context best rendered by "character" (in the sense of patterns of being and behaviour, but not necessarily with "moral" implications), to describe the ways music can convey, foster, and even generate emotional or mental states. Beyond this general description, there is no unified "Greek ethos theory" but "many different views, sometimes sharply opposed."[33] Ethos is attributed to the tonoi or harmoniai or modes (for instance, Plato, in the Republic (iii: 398d–399a), attributes "virility" to the "Dorian," and "relaxedness" to the "Lydian" mode), instruments (especially the aulos and the cithara, but also others), rhythms, and sometimes even the genus and individual tones. The most comprehensive treatment of musical ethos is provided by Aristides Quintilianus in his book On Music, with the original conception of assigning ethos to the various musical parameters according to the general categories of male and female. Aristoxenus was the first Greek theorist to point out that ethos does not only reside in the individual parameters but also in the musical piece as a whole (cited in Pseudo-Plutarch, De Musica 32: 1142d ff; see also Aristides Quintilianus 1.12). The Greeks were interested in musical ethos particularly in the context of education (so Plato in his Republic and Aristotle in his eighth book of his Politics), with implications for the well-being of the State. Many other ancient authors refer to what is nowadays called psychological effect of music and draw judgments for the appropriateness (or value) of particular musical features or styles, while others, in particular Philodemus (in his fragmentary work De musica) and Sextus Empiricus (in his sixth book of his work Adversus mathematicos), deny that music possesses any influence on the human person apart from generating pleasure. These different views anticipate in some way the modern debate in music philosophy whether music on its own or absolute music, independent of text, is able to elicit emotions on the listener or musician.[36]
Cleonides describes "melic" composition, "the employment of the materials subject to harmonic practice with due regard to the requirements of each of the subjects under consideration"[37] — which, together with the scales, tonoi, and harmoniai resemble elements found in medieval modal theory.[38] According to Aristides Quintilianus (On Music, i.12), melic composition is subdivided into three classes: dithyrambic, nomic, and tragic. These parallel his three classes of rhythmic composition: systaltic, diastaltic and hesychastic. Each of these broad classes of melic composition may contain various subclasses, such as erotic, comic and panegyric, and any composition might be elevating (diastaltic), depressing (systaltic), or soothing (hesychastic).[39]
The classification of the requirements we have from Proclus Useful Knowledge as preserved by Photios:
According to Mathiesen: