Background[edit]

The study of orbital motion and mathematical modeling of orbits began with the first attempts to predict planetary motions in the sky, although in ancient times the causes remained a mystery. Newton, at the time he formulated his laws of motion and of gravitation, applied them to the first analysis of perturbations,^[1] recognizing the complex difficulties of their calculation.^[1] Many of the great mathematicians since then have given attention to the various problems involved; throughout the 18th and 19th centuries there was demand for accurate tables of the position of the Moon and planets for purposes of navigation at sea.


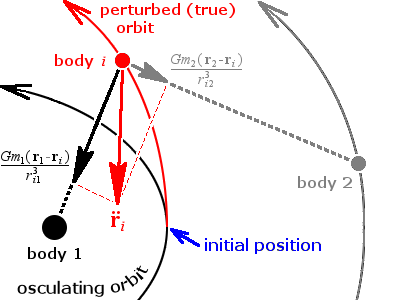
The complex motions of orbits can be broken down. The hypothetical motion that the body follows under the gravitational effect of one other body only is typically a conic section, and can be readily modeled with the methods of geometry. This is called a two-body problem, or an unperturbed Keplerian orbit. The differences between the Keplerian orbit and the actual motion of the body are caused by perturbations. These perturbations are caused by forces other than the gravitational effect between the primary and secondary body and must be modeled to create an accurate orbit simulation. Most orbit modeling approaches model the two-body problem and then add models of these perturbing forces and simulate these models over time. Perturbing forces may include gravitational attraction from other bodies besides the primary, solar wind, drag, magnetic fields, and propulsive forces.


Analytical solutions (mathematical expressions to predict the positions and motions at any future time) for simple two-body and three-body problems exist; none have been found for the n-body problem except for certain special cases. Even the two-body problem becomes insoluble if one of the bodies is irregular in shape.^[2]


Due to the difficulty in finding analytic solutions to most problems of interest, computer modeling and simulation is typically used to analyze orbital motion. A wide variety of software is available to simulate orbits and trajectories of spacecraft.