Riemann surface

In mathematics, particularly in complex analysis, a Riemann surface is a connected one-dimensional complex manifold. These surfaces were first studied by and are named after Bernhard Riemann. Riemann surfaces can be thought of as deformed versions of the complex plane: locally near every point they look like patches of the complex plane, but the global topology can be quite different. For example, they can look like a sphere or a torus or several sheets glued together.

Not to be confused with Riemannian surface or Riemannian manifold.

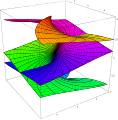
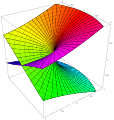
Examples of Riemann surfaces include graphs of multivalued functions like √z or log(z), e.g. the subset of pairs (z,w) ∈ C² with w = log(z).

Every Riemann surface is a surface: a two-dimensional real manifold, but it contains more structure (specifically a complex structure). Conversely, a two-dimensional real manifold can be turned into a Riemann surface (usually in several inequivalent ways) if and only if it is orientable and metrizable. Given this, the sphere and torus admit complex structures but the Möbius strip, Klein bottle and real projective plane do not. Every compact Riemann surface is a complex algebraic curve by Chow's theorem and the Riemann–Roch theorem.

$_$_$DEEZ_NUTS#0__titleDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#0__subtitleDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#0__call_to_action.textDEEZ_NUTS$_$_$

f(z) = arcsin z

f(z) = log z

f(z) = z^1/2

f(z) = z^1/3

f(z) = z^1/4

The Riemann sphere ${\widehat {\mathbf {C} }}:=\mathbf {C} \cup \{\infty \}$ , which is isomorphic to the ;

$\mathbf {P} ^{1}(\mathbf {C} )$

The complex plane $\mathbf {C}$ ;

The $\mathbf {D} :=\{z\in \mathbf {C} :|z|<1\}$ which is isomorphic to the upper half-plane $\mathbf {H} :=\{z\in \mathbf {C} :\mathrm {Im} (z)>0\}$ .

open disk

genus 0 – the isometry group of the sphere is the of projective transforms of the complex line,

Möbius group

the isometry group of the plane is the fixing infinity, and of the punctured plane is the subgroup leaving invariant the set containing only infinity and zero: either fixing them both, or interchanging them (1/z).

subgroup

the isometry group of the is the real Möbius group; this is conjugate to the automorphism group of the disk.

upper half-plane

genus 1 – the isometry group of a torus is in general translations (as an ), though the square lattice and hexagonal lattice have addition symmetries from rotation by 90° and 60°.

Abelian variety

For genus g ≥ 2, the isometry group is finite, and has order at most 84(g − 1), by ; surfaces that realize this bound are called Hurwitz surfaces.

Hurwitz's automorphisms theorem

[4]

Function-theoretic classification[edit]

The classification scheme above is typically used by geometers. There is a different classification for Riemann surfaces which is typically used by complex analysts. It employs a different definition for "parabolic" and "hyperbolic". In this alternative classification scheme, a Riemann surface is called parabolic if there are no non-constant negative subharmonic functions on the surface and is otherwise called hyperbolic.^[5]^[6] This class of hyperbolic surfaces is further subdivided into subclasses according to whether function spaces other than the negative subharmonic functions are degenerate, e.g. Riemann surfaces on which all bounded holomorphic functions are constant, or on which all bounded harmonic functions are constant, or on which all positive harmonic functions are constant, etc.

To avoid confusion, call the classification based on metrics of constant curvature the geometric classification, and the one based on degeneracy of function spaces the function-theoretic classification. For example, the Riemann surface consisting of "all complex numbers but 0 and 1" is parabolic in the function-theoretic classification but it is hyperbolic in the geometric classification.

$_$_$DEEZ_NUTS#7__descriptionDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#4__descriptionDEEZ_NUTS$_$_$

The isometry group of a uniformized Riemann surface (equivalently, the conformal automorphism group) reflects its geometry:

$_$_$DEEZ_NUTS#3__titleDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#3__descriptionDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#2__titleDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#2__descriptionDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#5__titleDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#5__descriptionDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#6__titleDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#6__descriptionDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#7__titleDEEZ_NUTS$_$_$

Dessin d'enfant

Kähler manifold

Lorentz surface

Mapping class group

Serre duality

, Encyclopedia of Mathematics, EMS Press, 2001 [1994]

"Riemann surface"

McMullen, C. (PDF). Harvard Math. Harvard University.

"Complex Analysis on Riemann Surfaces Math 213b"

$_$_$DEEZ_NUTS#8__titleDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#8__subtextDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#8__quote--0DEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#8__name--0DEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#8__company_or_position--0DEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#1__titleDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#1__subtextDEEZ_NUTS$_$_$

$_$_$DEEZ_NUTS#1__answer--0DEEZ_NUTS$_$_$