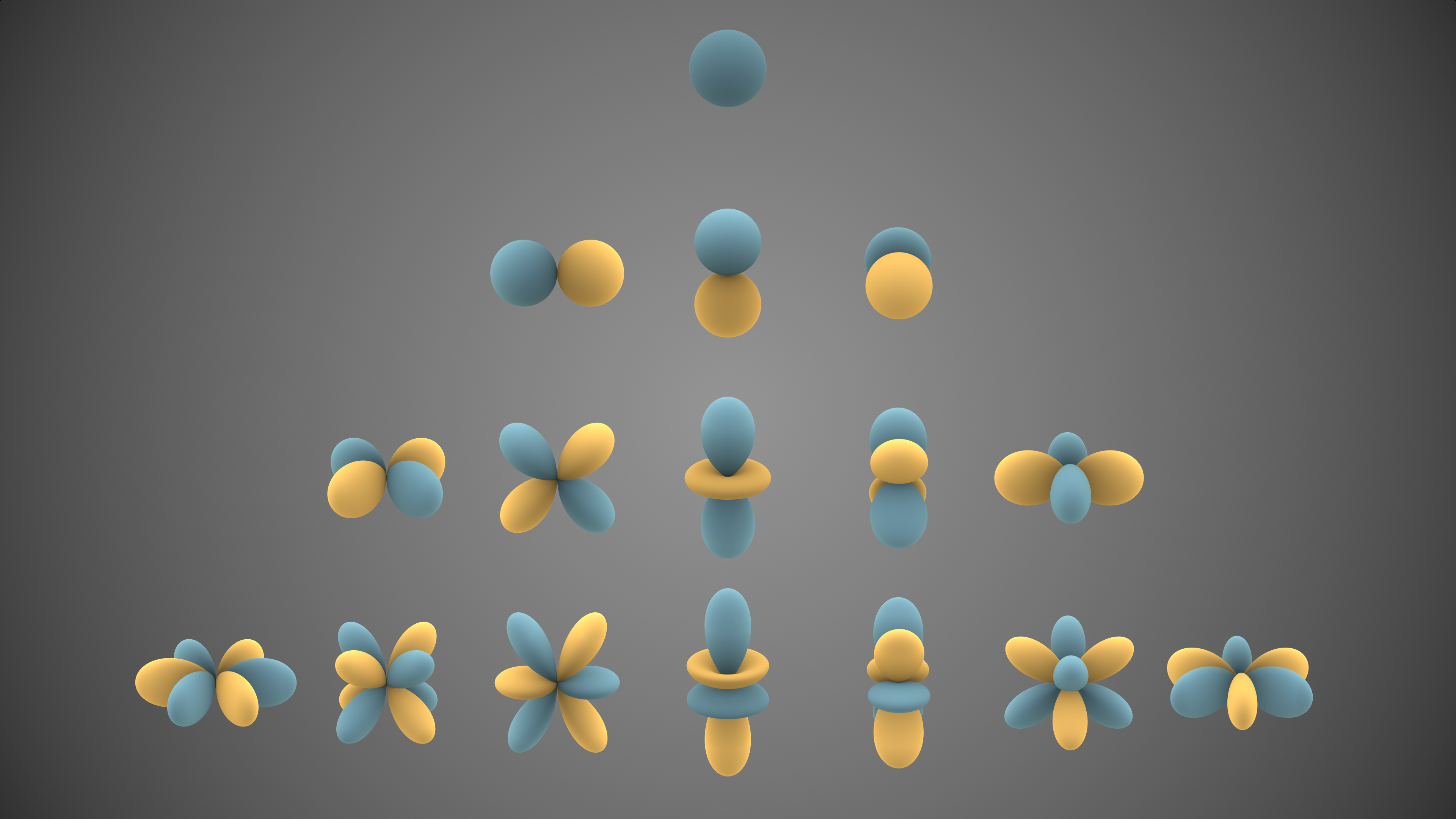
Spherical harmonics

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields. The table of spherical harmonics contains a list of common spherical harmonics.

"Ylm" redirects here. For other uses, see YLM (disambiguation).

Since the spherical harmonics form a complete set of orthogonal functions and thus an orthonormal basis, each function defined on the surface of a sphere can be written as a sum of these spherical harmonics. This is similar to periodic functions defined on a circle that can be expressed as a sum of circular functions (sines and cosines) via Fourier series. Like the sines and cosines in Fourier series, the spherical harmonics may be organized by (spatial) angular frequency, as seen in the rows of functions in the illustration on the right. Further, spherical harmonics are basis functions for irreducible representations of SO(3), the group of rotations in three dimensions, and thus play a central role in the group theoretic discussion of SO(3).

Spherical harmonics originate from solving Laplace's equation in the spherical domains. Functions that are solutions to Laplace's equation are called harmonics. Despite their name, spherical harmonics take their simplest form in Cartesian coordinates, where they can be defined as homogeneous polynomials of degree $\ell$ in $(x,y,z)$ that obey Laplace's equation. The connection with spherical coordinates arises immediately if one uses the homogeneity to extract a factor of radial dependence $r^{\ell }$ from the above-mentioned polynomial of degree $\ell$ ; the remaining factor can be regarded as a function of the spherical angular coordinates $\theta$ and $\varphi$ only, or equivalently of the orientational unit vector $\mathbf {r}$ specified by these angles. In this setting, they may be viewed as the angular portion of a set of solutions to Laplace's equation in three dimensions, and this viewpoint is often taken as an alternative definition. Notice, however, that spherical harmonics are not functions on the sphere which are harmonic with respect to the Laplace-Beltrami operator for the standard round metric on the sphere: the only harmonic functions in this sense on the sphere are the constants, since harmonic functions satisfy the Maximum principle. Spherical harmonics, as functions on the sphere, are eigenfunctions of the Laplace-Beltrami operator (see the section Higher dimensions below).

A specific set of spherical harmonics, denoted $Y_{\ell }^{m}(\theta ,\varphi )$ or $Y_{\ell }^{m}({\mathbf {r} })$ , are known as Laplace's spherical harmonics, as they were first introduced by Pierre Simon de Laplace in 1782.^[1] These functions form an orthogonal system, and are thus basic to the expansion of a general function on the sphere as alluded to above.

Spherical harmonics are important in many theoretical and practical applications, including the representation of multipole electrostatic and electromagnetic fields, electron configurations, gravitational fields, geoids, the magnetic fields of planetary bodies and stars, and the cosmic microwave background radiation. In 3D computer graphics, spherical harmonics play a role in a wide variety of topics including indirect lighting (ambient occlusion, global illumination, precomputed radiance transfer, etc.) and modelling of 3D shapes.

Algebraic properties[edit]

Addition theorem[edit]

A mathematical result of considerable interest and use is called the addition theorem for spherical harmonics. Given two vectors $r$ and $r'$ , with spherical coordinates $(r,\theta ,\varphi )$ and $(r',\theta ',\varphi ')$ , respectively, the angle $\gamma$ between them is given by the relation

The sum of the spaces $H ℓ$ is in the set $C(S^{n-1})$ of continuous functions on $S^{n-1}$ with respect to the uniform topology, by the Stone–Weierstrass theorem. As a result, the sum of these spaces is also dense in the space $L 2 (S n -1)$ of square-integrable functions on the sphere. Thus every square-integrable function on the sphere decomposes uniquely into a series of spherical harmonics, where the series converges in the $L 2$ sense.

dense

For all $f \in H ℓ$ , one has
$\Delta _{S^{n-1}}f=-\ell (\ell +n-2)f.$ where $Δ S n -1$ is the on $S n -1$ . This operator is the analog of the angular part of the Laplacian in three dimensions; to wit, the Laplacian in $n$ dimensions decomposes as $\nabla ^{2}=r^{1-n}{\frac {\partial }{\partial r}}r^{n-1}{\frac {\partial }{\partial r}}+r^{-2}\Delta _{S^{n-1}}={\frac {\partial ^{2}}{\partial r^{2}}}+{\frac {n-1}{r}}{\frac {\partial }{\partial r}}+r^{-2}\Delta _{S^{n-1}}$

Laplace–Beltrami operator

It follows from the and the preceding property that the spaces $H ℓ$ are orthogonal with respect to the inner product from $L 2 (S n -1)$ . That is to say,
$\int _{S^{n-1}}f{\bar {g}}\,\mathrm {d} \Omega =0$ for $f \in H ℓ$ and $g \in H k$ for $k \neq ℓ$ .

Stokes theorem

Conversely, the spaces $H ℓ$ are precisely the eigenspaces of $Δ S n -1$ . In particular, an application of the to the Riesz potential $\Delta _{S^{n-1}}^{-1}$ gives another proof that the spaces $H ℓ$ are pairwise orthogonal and complete in $L 2 (S n -1)$ .

spectral theorem

Every homogeneous polynomial $p \in P ℓ$ can be uniquely written in the form
$p(x)=p_{\ell }(x)+|x|^{2}p_{\ell -2}+\cdots +{\begin{cases}|x|^{\ell }p_{0}&\ell {\rm {\ even}}\\|x|^{\ell -1}p_{1}(x)&\ell {\rm {\ odd}}\end{cases}}$ where $p j \in A j$ . In particular, $\dim \mathbf {H} _{\ell }={\binom {n+\ell -1}{n-1}}-{\binom {n+\ell -3}{n-1}}={\binom {n+\ell -2}{n-2}}+{\binom {n+\ell -3}{n-2}}.$

[25]

The classical spherical harmonics are defined as complex-valued functions on the unit sphere $S^{2}$ inside three-dimensional Euclidean space $\mathbb {R} ^{3}$ . Spherical harmonics can be generalized to higher-dimensional Euclidean space $\mathbb {R} ^{n}$ as follows, leading to functions $S^{n-1}\to \mathbb {C}$ .^[24] Let P_ℓ denote the space of complex-valued homogeneous polynomials of degree $ℓ$ in $n$ real variables, here considered as functions $\mathbb {R} ^{n}\to \mathbb {C}$ . That is, a polynomial $p$ is in $P ℓ$ provided that for any real $\lambda \in \mathbb {R}$ , one has

Let A_ℓ denote the subspace of P_ℓ consisting of all harmonic polynomials:

The following properties hold:

An orthogonal basis of spherical harmonics in higher dimensions can be constructed inductively by the method of separation of variables, by solving the Sturm-Liouville problem for the spherical Laplacian

; Hilbert, David (1962), Methods of Mathematical Physics, Volume I, Wiley-Interscience.

Courant, Richard

Edmonds, A.R. (1957), , Princeton University Press, ISBN 0-691-07912-9

Angular Momentum in Quantum Mechanics

Eremenko, Alexandre; Jakobson, Dmitry; Nadirashvili, Nikolai (2007), , Annales de l'Institut Fourier, 57 (7): 2345–2360, doi:10.5802/aif.2335, ISSN 0373-0956, MR 2394544

"On nodal sets and nodal domains on S² and R²"

Hall, Brian C. (2013), Quantum Theory for Mathematicians, Graduate Texts in Mathematics, vol. 267, Springer, 978-1461471158

ISBN

MacRobert, T.M. (1967), Spherical harmonics: An elementary treatise on harmonic functions, with applications, Pergamon Press.

Meijer, Paul Herman Ernst; Bauer, Edmond (2004), Group theory: The application to quantum mechanics, Dover, 978-0-486-43798-9.

ISBN

Solomentsev, E.D. (2001) [1994], , Encyclopedia of Mathematics, EMS Press.

"Spherical harmonics"

; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton, N.J.: Princeton University Press, ISBN 978-0-691-08078-9.

Stein, Elias

Unsöld, Albrecht (1927), "Beiträge zur Quantenmechanik der Atome", Annalen der Physik, 387 (3): 355–393, :1927AnP...387..355U, doi:10.1002/andp.19273870304.

Bibcode

; Watson, G. N. (1927), A Course of Modern Analysis, Cambridge University Press, p. 392.

Whittaker, E. T.

at MathWorld

Spherical harmonics

Algebraic properties[edit]

Addition theorem[edit]

dense

Laplace–Beltrami operator

Stokes theorem

spectral theorem

[25]

Courant, Richard

Angular Momentum in Quantum Mechanics

"On nodal sets and nodal domains on S² and R²"

ISBN

ISBN

"Spherical harmonics"

Stein, Elias

Bibcode

Whittaker, E. T.

Spherical Harmonics

Spherical Harmonics 3D representation