Vanishing point
A vanishing point is a point on the image plane of a perspective rendering where the two-dimensional perspective projections of mutually parallel lines in three-dimensional space appear to converge. When the set of parallel lines is perpendicular to a picture plane, the construction is known as one-point perspective, and their vanishing point corresponds to the oculus, or "eye point", from which the image should be viewed for correct perspective geometry.[1] Traditional linear drawings use objects with one to three sets of parallels, defining one to three vanishing points.
For other uses, see Vanishing point (disambiguation).Italian humanist polymath and architect Leon Battista Alberti first introduced the concept in his treatise on perspective in art, De pictura, written in 1435.[2] Straight railroad tracks are a familiar modern example.[3]
Theorem[edit]
The vanishing point theorem is the principal theorem in the science of perspective. It says that the image in a picture plane π of a line L in space, not parallel to the picture, is determined by its intersection with π and its vanishing point. Some authors have used the phrase, "the image of a line includes its vanishing point". Guidobaldo del Monte gave several verifications, and Humphry Ditton called the result the "main and Great Proposition".[5] Brook Taylor wrote the first book in English on perspective in 1714, which introduced the term "vanishing point" and was the first to fully explain the geometry of multipoint perspective, and historian Kirsti Andersen compiled these observations.[1]: 244–6 She notes, in terms of projective geometry, the vanishing point is the image of the point at infinity associated with L, as the sightline from O through the vanishing point is parallel to L.
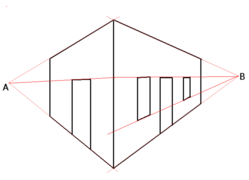
Vanishing line[edit]
As a vanishing point originates in a line, so a vanishing line originates in a plane α that is not parallel to the picture π. Given the eye point O, and β the plane parallel to α and lying on O, then the vanishing line of α is β ∩ π. For example, when α is the ground plane and β is the horizon plane, then the vanishing line of α is the horizon line β ∩ π.
To put it simply, the vanishing line of some plane, say α, is obtained by the intersection of the image plane with another plane, say β, parallel to the plane of interest (α), passing through the camera center. For different sets of lines parallel to this plane α, their respective vanishing points will lie on this vanishing line. The horizon line is a theoretical line that represents the eye level of the observer. If the object is below the horizon line, its lines angle up to the horizon line. If the object is above, they slope down.
A curvilinear perspective is a drawing with either 4 or 5 vanishing points. In 5-point perspective the vanishing points are mapped into a circle with 4 vanishing points at the cardinal headings N, W, S, E and one at the circle's origin.
A reverse perspective is a drawing with vanishing points that are placed outside the painting with the illusion that they are "in front of" the painting.
Detection[edit]
Several methods for vanishing point detection make use of the line segments detected in images. Other techniques involve considering the intensity gradients of the image pixels directly.
There are significantly large numbers of vanishing points present in an image. Therefore, the aim is to detect the vanishing points that correspond to the principal directions of a scene. This is generally achieved in two steps. The first step, called the accumulation step, as the name suggests, clusters the line segments with the assumption that a cluster will have a common vanishing point. The next step finds the principal clusters present in the scene and therefore it is called the search step.
In the accumulation step, the image is mapped onto a bounded space called the accumulator space. The accumulator space is partitioned into units called cells. Barnard[6] assumed this space to be a Gaussian sphere centered on the optical center of the camera as an accumulator space. A line segment on the image corresponds to a great circle on this sphere, and the vanishing point in the image is mapped to a point. The Gaussian sphere has accumulator cells that increase when a great circle passes through them, i.e. in the image a line segment intersects the vanishing point. Several modifications have been made since, but one of the most efficient techniques was using the Hough Transform, mapping the parameters of the line segment to the bounded space. Cascaded Hough Transforms have been applied for multiple vanishing points.
The process of mapping from the image to the bounded spaces causes the loss of the actual distances between line segments and points.
In the search step, the accumulator cell with the maximum number of line segments passing through it is found. This is followed by removal of those line segments, and the search step is repeated until this count goes below a certain threshold. As more computing power is now available, points corresponding to two or three mutually orthogonal directions can be found.