Improper integral

In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral.^[1] In the context of Riemann integrals (or, equivalently, Darboux integrals), this typically involves unboundedness, either of the set over which the integral is taken or of the integrand (the function being integrated), or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge.^[2]^[1] If a regular definite integral (which may retronymically be called a proper integral) is worked out as if it is improper, the same answer will result.

In the simplest case of a real-valued function of a single variable integrated in the sense of Riemann (or Darboux) over a single interval, improper integrals may be in any of the following forms:

The first three forms are improper because the integrals are taken over an unbounded interval. (They may be improper for other reasons, as well, as explained below.) Such an integral is sometimes described as being of the "first" type or kind if the integrand otherwise satisfies the assumptions of integration.^[2] Integrals in the fourth form that are improper because $f(x)$ has a vertical asymptote somewhere on the interval $[a,b]$ may be described as being of the "second" type or kind.^[2] Integrals that combine aspects of both types are sometimes described as being of the "third" type or kind.^[2]

In each case above, the improper integral must be rewritten using one or more limits, depending on what is causing the integral to be improper. For example, in case 1, if $f(x)$ is continuous on the entire interval $[a,\infty )$ , then

The limit on the right is taken to be the definition of the integral notation on the left.

If $f(x)$ is only continuous on $(a,\infty )$ and not at $a$ itself, then typically this is rewritten as

for any choice of $c>a$ . Here both limits must converge to a finite value for the improper integral to be said to converge. This requirement avoids the ambiguous case of adding positive and negative infinities (i.e., the " $\infty -\infty$ " indeterminate form). Alternatively, an iterated limit could be used or a single limit based on the Cauchy principal value.

If $f(x)$ is continuous on $[a,d)$ and $(d,\infty )$ , with a discontinuity of any kind at $d$ , then

for any choice of $c>d$ . The previous remarks about indeterminate forms, iterated limits, and the Cauchy principal value also apply here.

The function $f(x)$ can have more discontinuities, in which case even more limits would be required (or a more complicated principal value expression).

Cases 2–4 are handled similarly. See the examples below.

Improper integrals can also be evaluated in the context of complex numbers, in higher dimensions, and in other theoretical frameworks such as Lebesgue integration or Henstock–Kurzweil integration. Integrals that are considered improper in one framework may not be in others.

Does the limit exist?

Can the limit be computed?

An improper integral converges if the limit defining it exists. Thus for example one says that the improper integral

exists and is equal to L if the integrals under the limit exist for all sufficiently large t, and the value of the limit is equal to L.

It is also possible for an improper integral to diverge to infinity. In that case, one may assign the value of ∞ (or −∞) to the integral. For instance

However, other improper integrals may simply diverge in no particular direction, such as

which does not exist, even as an extended real number. This is called divergence by oscillation.

A limitation of the technique of improper integration is that the limit must be taken with respect to one endpoint at a time. Thus, for instance, an improper integral of the form

can be defined by taking two separate limits; to which

provided the double limit is finite. It can also be defined as a pair of distinct improper integrals of the first kind:

where c is any convenient point at which to start the integration. This definition also applies when one of these integrals is infinite, or both if they have the same sign.

An example of an improper integral where both endpoints are infinite is the Gaussian integral ${\textstyle \int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}}$ . An example which evaluates to infinity is ${\textstyle \int _{-\infty }^{\infty }e^{x}\,dx}$ . But one cannot even define other integrals of this kind unambiguously, such as ${\textstyle \int _{-\infty }^{\infty }x\,dx}$ , since the double limit is infinite and the two-integral method

yields an indeterminate form, $\infty -\infty$ . In this case, one can however define an improper integral in the sense of Cauchy principal value:

The questions one must address in determining an improper integral are:

The first question is an issue of mathematical analysis. The second one can be addressed by calculus techniques, but also in some cases by contour integration, Fourier transforms and other more advanced methods.

For the Riemann integral (or the , which is equivalent to it), improper integration is necessary both for unbounded intervals (since one cannot divide the interval into finitely many subintervals of finite length) and for unbounded functions with finite integral (since, supposing it is unbounded above, then the upper integral will be infinite, but the lower integral will be finite).

Darboux integral

The deals differently with unbounded domains and unbounded functions, so that often an integral which only exists as an improper Riemann integral will exist as a (proper) Lebesgue integral, such as ${\textstyle \int _{1}^{\infty }{\frac {dx}{x^{2}}}}$ . On the other hand, there are also integrals that have an improper Riemann integral but do not have a (proper) Lebesgue integral, such as ${\textstyle \int _{0}^{\infty }{\frac {\sin x}{x}}\,dx}$ . The Lebesgue theory does not see this as a deficiency: from the point of view of measure theory, ${\textstyle \int _{0}^{\infty }{\frac {\sin x}{x}}\,dx=\infty -\infty }$ and cannot be defined satisfactorily. In some situations, however, it may be convenient to employ improper Lebesgue integrals as is the case, for instance, when defining the Cauchy principal value. The Lebesgue integral is more or less essential in the theoretical treatment of the Fourier transform, with pervasive use of integrals over the whole real line.

Lebesgue integral

For the , improper integration is not necessary, and this is seen as a strength of the theory: it encompasses all Lebesgue integrable and improper Riemann integrable functions.

Henstock–Kurzweil integral

There is more than one theory of integration. From the point of view of calculus, the Riemann integral theory is usually assumed as the default theory. In using improper integrals, it can matter which integration theory is in play.

If a function f is Riemann integrable on [a,b] for every b ≥ a, and the partial integrals

In some cases, the integral

can be defined as an integral (a Lebesgue integral, for instance) without reference to the limit

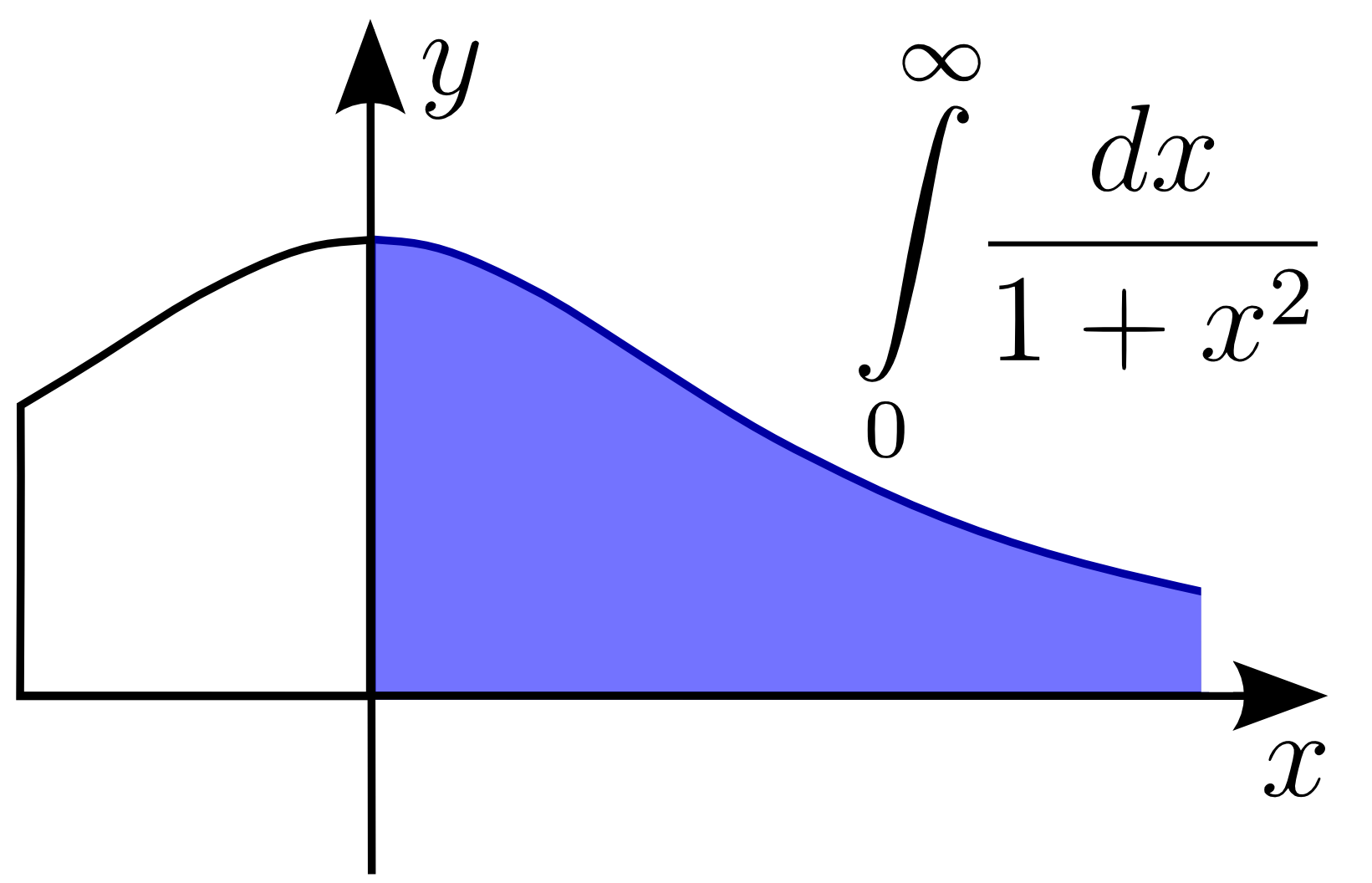
but cannot otherwise be conveniently computed. This often happens when the function f being integrated from a to c has a vertical asymptote at c, or if c = ∞ (see Figures 1 and 2). In such cases, the improper Riemann integral allows one to calculate the Lebesgue integral of the function. Specifically, the following theorem holds (Apostol 1974, Theorem 10.33):

For example, the integral

can be interpreted alternatively as the improper integral

or it may be interpreted instead as a Lebesgue integral over the set (0, ∞). Since both of these kinds of integral agree, one is free to choose the first method to calculate the value of the integral, even if one ultimately wishes to regard it as a Lebesgue integral. Thus improper integrals are clearly useful tools for obtaining the actual values of integrals.

In other cases, however, a Lebesgue integral between finite endpoints may not even be defined, because the integrals of the positive and negative parts of f are both infinite, but the improper Riemann integral may still exist. Such cases are "properly improper" integrals, i.e. their values cannot be defined except as such limits. For example,

cannot be interpreted as a Lebesgue integral, since

But $f(x)={\frac {\sin(x)}{x}}$ is nevertheless integrable between any two finite endpoints, and its integral between 0 and ∞ is usually understood as the limit of the integral:

Singularities[edit]

One can speak of the singularities of an improper integral, meaning those points of the extended real number line at which limits are used.

(1974), Mathematical analysis, Addison-Wesley, ISBN 978-0-201-00288-1.

Apostol, T

(1967), Calculus, Vol. 1 (2nd ed.), Jon Wiley & Sons.

Apostol, T

Autar Kaw, Egwu Kalu (2008), (1st ed.), autarkaw.com

Numerical Methods with Applications

(1948), Introduction to the theory of Fourier integrals (2nd ed.), New York, N.Y.: Chelsea Pub. Co. (published 1986), ISBN 978-0-8284-0324-5.

Titchmarsh, E

Cooper, Jeffery (2005), Working analysis, Gulf Professional

Ghorpade, Sudhir; Limaye, Balmohan (2010), A course in multivariable calculus and analysis, Springer

at Holistic Numerical Methods Institute

Improper integral

Darboux integral

Lebesgue integral

Henstock–Kurzweil integral

Singularities[edit]

Apostol, T

Apostol, T

Numerical Methods with Applications

Titchmarsh, E

Numerical Methods to Solve Improper Integrals